IMP modules.IMP has a number of geometry primitives. They support the following namespace functions as appropriateIMP are written to work in any dimension. In C++, this is implemented via templates (such as IMP::algebra::VectorD). In the python side, the different dimensions are named explicitly instead. That means, a 2-D point is IMP::algebra::VectorD<2> in C++, and IMP::algbra::Vector2D in python and the function IMP::algebra::get_basis_vector_d<3>() in C++ becomes IMP.algebra.get_basis_vector_3d() in Python. Similarly, a collection of 2D points is std::vector<IMP::algebra::VectorD<2> > in C++ and IMP.algebra.Vector2Ds in python, which as with all collections, look like python lists. For convenience, we provide typedefs in C++ to the IMP::algbra::Vector2D and IMP::algebra::Vector2Ds style names.IMP::algebra::VectorD<3> v0, v1; v0 != v1; // only legal operations initialize v0, eg v0= IMP::algebra::VectorD<3>(1,2,3);
IMP requires or benefits from using CGAL. CGAL is a library of geometry-related algorithms and data structures written in C++. The relevant parts of CGAL are licensed under LGPL and QPL and commercial licenses are available if needed. More information can be found on the CGAL license page.IMP and how to apply them to biological problems.
Data Structures | |
| class | BoundingBoxD |
| An axis-aligned bounding box. More... | |
| class | Cone3D |
| class | Cylinder3D |
| class | Ellipsoid3D |
| class | FixedXYZ |
| A simple class for returning XYZ Euler angles. More... | |
| class | FixedZYZ |
| A simple class for returning ZYZ Euler angles. More... | |
| class | Grid3D |
| A voxel grid in 3D space. More... | |
| class | GridRangeD |
| A Boost.Range over the vertices of a grid. More... | |
| class | LinearFit |
| Calculate line that fits best the input data points. More... | |
| class | Matrix2D |
| class | Matrix3D |
| class | MultiArray |
| class | NearestNeighborD |
| class | ParabolicFit |
| Calculate parabola that fits best the input data points. More... | |
| class | Plane3D |
| class | Rotation2D |
| Stores a 2D rotation matrix. More... | |
| class | Rotation3D |
| 3D rotation class. More... | |
| class | Segment3D |
| class | SphereD |
| class | SpherePatch3D |
| class | SphericalVector3D |
| Class to represent a 3D point in spherical coordinates. More... | |
| class | Transformation2D |
| Simple 2D transformation class. More... | |
| class | Transformation3D |
| Simple 3D transformation class. More... | |
| class | VectorD |
| A Cartesian vector in D-dimensions. More... | |
Typedefs | |
|
typedef std::pair< VectorD < 3 >, double > | AxisAnglePair |
| typedef BoundingBoxD< 3 > | BoundingBoxD< 3 > |
|
typedef Matrix2D< std::complex < double > > | Matrix2D_c |
| typedef Matrix2D< double > | Matrix2D_d |
| typedef Matrix2D< int > | Matrix2D_i |
|
typedef VectorOfRefCounted < Matrix2D_c * > | Matrix2Ds_c |
|
typedef VectorOfRefCounted < Matrix2D_d * > | Matrix2Ds_d |
| A vector of reference counted pointers to 2D Matrices of doubles. | |
| typedef std::vector< Rotation3D > | Rotation3Ds |
| typedef VectorD< 2 > | Vector2D |
| typedef std::vector< VectorD< 2 > > | Vector2Ds |
| typedef VectorD< 3 > | Vector3D |
| typedef std::vector< VectorD< 3 > > | Vector3Ds |
| typedef VectorD< 4 > | Vector4D |
| typedef std::vector< VectorD< 4 > > | Vector4Ds |
Functions | |
| template<unsigned int D> | |
| int | compare (const VectorD< D > &a, const VectorD< D > &b) |
| lexicographic comparison of two vectors | |
| Transformation3D | compose (const Transformation3D &a, const Transformation3D &b) |
| compose two transformations | |
| Transformation2D | compose (const Transformation2D &a, const Transformation2D &b) |
| compose two transformations | |
| Rotation3D | compose (const Rotation3D &a, const Rotation3D &b) |
| Rotation2D | compose (const Rotation2D &a, const Rotation2D &b) |
| compose two rotations a and b | |
| bool | get_are_almost_equal (const double a, const double b, const double epsilon) |
| Compares two values (intended for doubles). | |
| template<class Geometry > | |
| double | get_area (const Geometry &) |
| Compute the area of any surface object. | |
| std::pair< VectorD< 3 >, double > | get_axis_and_angle (const Rotation3D &rot) |
| Decompose a Rotation3D object into a rotation around an axis. | |
| double | get_ball_radius_from_volume_3d (double volume) |
| Return the radius of a sphere with a given volume. | |
| template<unsigned int D> | |
| VectorD< D > | get_basis_vector_d (unsigned int coordinate) |
| Return the basis vector for the given coordinate. | |
| template<class Geometry > | |
| BoundingBoxD< 3 > | get_bounding_box (const Geometry &) |
| Compute the bounding box of any geometric object. | |
| template<typename T > | |
| T | get_constrained (const T x, const T x0, const T xF) |
| Constrains a value between two given limits. | |
| std::string | get_data_path (std::string file_name) |
| Return the path to installed data for this module. | |
| template<unsigned int D> | |
| double | get_distance (const VectorD< D > &v1, const VectorD< D > &v2) |
| compute the distance between two vectors | |
| template<unsigned int D> | |
| double | get_distance (const SphereD< D > &a, const SphereD< D > &b) |
| Return the distance between the two spheres if they are disjoint. | |
| double | get_distance (const Segment3D &a, const Segment3D &b) |
| Get the distance between two segments. | |
| double | get_distance (const Segment3D &s, const VectorD< 3 > &p) |
| Get the distance between a segment and a point. | |
| double | get_distance (const Rotation3D &r0, const Rotation3D &r1) |
| Return a distance between the two rotations. | |
| double | get_distance (const Plane3D &pln, const VectorD< 3 > &p) |
| Return the distance between a plane and a point in 3D. | |
| SphereD< 3 > | get_enclosing_sphere (const std::vector< VectorD< 3 > > &ss) |
| Return a sphere containing the listed spheres. | |
| SphereD< 3 > | get_enclosing_sphere (const std::vector< SphereD< 3 > > &ss) |
| Return a sphere containing the listed spheres. | |
| std::string | get_example_path (std::string file_name) |
| Return the path to installed example data for this module. | |
| const VectorD< 3 > & | get_geometry (const VectorD< 3 > &v) |
| Rotation2D | get_identity_rotation_2d () |
| Builds an identity rotation in 2D. | |
| Rotation3D | get_identity_rotation_3d () |
| Return a rotation that does not do anything. | |
| Transformation2D | get_identity_transformation_2d () |
| Returns a transformation that does not do anything. | |
| Transformation3D | get_identity_transformation_3d () |
| Return a transformation that does not do anything. | |
| template<unsigned int D> | |
| bool | get_interiors_intersect (const SphereD< D > &a, const SphereD< D > &b) |
| Return true if the two balls bounded by the two spheres interesect. | |
| template<typename T > | |
| T | get_linearly_interpolated (double diff, T lower, T upper) |
| Simple interpolation that is only valid for values of a ranging from 0 to 1. | |
| std::string | get_module_name () |
| const VersionInfo & | get_module_version_info () |
| double | get_next_larger_power_of_2 (double x) |
| Closest power of 2 that can contain a number x. | |
| float | get_next_larger_power_of_2 (float x) |
| Closest power of 2 that can contain a number x. | |
| template<unsigned int D> | |
| VectorD< D > | get_ones_vector_d (double v=1) |
| Return a vector of ones (or another constant). | |
| template<unsigned int D> | |
| double | get_power_distance (const SphereD< D > &a, const SphereD< D > &b) |
| Return the power distance between the two spheres. | |
| PrincipalComponentAnalysis | get_principal_components (const std::vector< VectorD< 3 > > &ps) |
| Perform principle components analysis on a set of vectors. | |
| Rotation2D | get_random_rotation_2d () |
| Builds an identity rotation in 2D. | |
| Rotation3D | get_random_rotation_3d (const Rotation3D ¢er, double distance) |
| Pick a rotation at random near the provided one. | |
| Rotation3D | get_random_rotation_3d () |
| Pick a rotation at random from all possible rotations. | |
| Transformation3D | get_rotation_about_point (const VectorD< 3 > &point, const Rotation3D &rotation) |
| Generate a Transformation3D object from a rotation around a point. | |
| Transformation2D | get_rotation_about_point (const VectorD< 2 > &point, const Rotation2D &rotation) |
| Generates a Transformation2D object from a rotation around a point. | |
| Rotation3D | get_rotation_from_matrix (double m00, double m01, double m02, double m10, double m11, double m12, double m20, double m21, double m22) |
| Generate a Rotation3D object from a rotation matrix. | |
| Rotation3D | get_rotation_from_vector4d (const VectorD< 4 > &v) |
| Compute a rotatation from an unnormalized quaternion. | |
| Rotation3D | get_rotation_in_radians_about_axis (const VectorD< 3 > &axis, double angle) |
| Generate a Rotation3D object from a rotation around an axis. | |
| Rotation3D | get_rotation_taking_first_to_second (const VectorD< 3 > &v1, const VectorD< 3 > &v2) |
| Create a rotation from the first vector to the second one. | |
| Rotation2D | get_rotation_to_x_axis (const VectorD< 2 > &v) |
| template<typename T > | |
| int | get_rounded (const T &x) |
| Rounds a number to next integer. | |
| template<typename T > | |
| int | get_sign (const T &x) |
| Sign of a number. 1 if the number is higher or equal to 0 and -1 otherwise. | |
| template<unsigned int D> | |
| double | get_squared_distance (const VectorD< D > &v1, const VectorD< D > &v2) |
| compute the squared distance between two vectors | |
| template<class Geometry > | |
| double | get_surface_area (const Geometry &) |
| Compute the surface area of any volumetric object. | |
| Transformation3D | get_transformation_3d (const Transformation2D &t2d) |
| Builds a 3D transformation from a 2D one. | |
| template<class Vector3DsOrXYZs0 , class Vector3DsOrXYZs1 > | |
| IMP::algebra::Transformation3D | get_transformation_aligning_first_to_second (const Vector3DsOrXYZs0 &from, const Vector3DsOrXYZs1 &to) |
| Compute the rigid transform bringing the first point set to the second. | |
| Transformation2D | get_transformation_aligning_pair (const std::vector< VectorD< 2 > > &set_from, const std::vector< VectorD< 2 > > &set_to) |
| Transformation3D | get_transformation_from_reference_frame (const VectorD< 3 > &u, const VectorD< 3 > &w, const VectorD< 3 > &base) |
| A rotation from the natural reference frame to one defined by u,w and base. The x-axis lies on u-base. The y-axis is perpendicular to both x and z. The z-axis is perpendicular to the u-base , w-base plane. | |
| BoundingBoxD< 3 > | get_transformed (const BoundingBoxD< 3 > &bb, const Transformation3D &tr) |
| Return a bounding box containing the transformed box. | |
| Rotation3Ds | get_uniform_cover_rotations_3d (unsigned int num_points) |
| Cover the space of rotations evenly. | |
| template<unsigned int D> | |
| BoundingBoxD< D > | get_unit_bounding_box_d () |
| template<unsigned int D> | |
| SphereD< D > | get_unit_sphere_d () |
| template<class Geometry > | |
| double | get_volume (const Geometry &) |
| Compute the volume of any volumetric object. | |
| template<unsigned int D> | |
| VectorD< D > | get_zero_vector_d () |
| Return a vector of zeros. | |
| Rotation3D | interpolate (const Rotation3D &a, const Rotation3D &b, double f) |
| Interpolate between two rotations. | |
| template<typename T , typename H > | |
| T | linear_interpolation (H &v, int size, double idx) |
| Linear interpolation for a point in a vector. | |
| template<unsigned int D> | |
| VectorD< D > | operator* (double s, const VectorD< D > &o) |
| bool | xorT (bool x, bool y) |
| xor operation between two values | |
3D Vectors | |
| VectorD< 3 > | get_centroid (const std::vector< VectorD< 3 > > &ps) |
| Returns the centroid of a set of vectors. | |
| VectorD< 3 > | get_orthogonal_vector (const VectorD< 3 > &v) |
| Return a vector that is perpendicular to the given vector. | |
| VectorD< 3 > | get_vector_product (const VectorD< 3 > &p1, const VectorD< 3 > &p2) |
| Returns the vector product (cross product) of two vectors. | |
Euler Angles | |
There are many conventions for how to define Euler angles, based on choices of which of the x,y,z axis to use in what order and whether the rotation axis is in the body frame (and hence affected by previous rotations) or in in a fixed frame. See http://en.wikipedia.org/wiki/Conversion_between_quaternions_and_Euler_angles for a general description.
| |
| FixedXYZ | get_fixed_xyz_from_rotation (const Rotation3D &r) |
| The inverse of rotation_from_fixed_xyz(). | |
| FixedZYZ | get_fixed_zyz_from_rotation (const Rotation3D &r) |
| The inverse of rotation_from_fixed_zyz(). | |
| Rotation3D | get_rotation_from_fixed_xyz (double xr, double yr, double zr) |
| Initialize a rotation in x-y-z order from three angles. | |
| Rotation3D | get_rotation_from_fixed_zxz (double phi, double theta, double psi) |
| Initialize a rotation from euler angles. | |
| Rotation3D | get_rotation_from_fixed_zyz (double Rot, double Tilt, double Psi) |
| Generate a rotation object from Euler Angles. | |
Vector Generators | |
These functions generate vector objects. Some of the methods, those with random in their name, generate a single vector chosen uniformly from the specified domain. Others, the cover methods, generate a set of points distributed (somewhat) evenly over the domain. | |
| std::vector< VectorD< 3 > > | get_grid_surface_cover (const Cylinder3D &cyl, int number_of_cycles, int number_of_points_on_cycle) |
| Generate a grid of 3d points on a cylinder surface. | |
| std::vector< VectorD< 3 > > | get_random_chain (unsigned int n, double r, const VectorD< 3 > &start=Vector3D(0, 0, 0), const std::vector< SphereD< 3 > > &obstacles=Sphere3Ds()) |
| Generate a random chain with no collisions. | |
| template<unsigned int D> | |
| VectorD< D > | get_random_vector_in (const SphereD< D > &s) |
| Generate a random vector in a sphere with uniform density. | |
| template<unsigned int D> | |
| VectorD< D > | get_random_vector_in (const BoundingBoxD< D > &bb) |
| Generate a random vector in a box with uniform density. | |
| template<unsigned int D> | |
| VectorD< D > | get_random_vector_on (const SphereD< D > &s) |
| Generate a random vector on a sphere with uniform density. | |
| template<unsigned int D> | |
| VectorD< D > | get_random_vector_on (const BoundingBoxD< D > &bb) |
| Generate a random vector on a box with uniform density. | |
| std::vector< VectorD< 3 > > | get_uniform_surface_cover (const Cone3D &cone, unsigned int number_of_points) |
| std::vector< VectorD< 3 > > | get_uniform_surface_cover (const SpherePatch3D &sph, unsigned int number_of_points) |
| Generate a set of 3d points that uniformly cover a patch of a sphere. | |
| std::vector< VectorD< 3 > > | get_uniform_surface_cover (const Cylinder3D &cyl, int number_of_points) |
| Generate a set of 3d points that uniformly cover a cylinder. | |
| template<unsigned int D> | |
| std::vector< VectorD< D > > | get_uniform_surface_cover (const SphereD< D > &s, unsigned int n) |
| Generate a set of vectors which covers a sphere uniformly. | |
| template<unsigned int D> | |
| std::vector< VectorD< D > > | get_uniform_upper_hemisphere_cover (const SphereD< D > &s, unsigned int n) |
| Generate a set of 3D points that uniformly cover a hemisphere. | |
Endian | |
IMP provides a variety of functionality to manage byte order in input and output data. | |
| bool | get_is_big_endian () |
| Returns 1 if machine is big endian else 0. | |
| bool | get_is_little_endian () |
| Returns 1 if machine is little endian else 0. | |
| template<class T > | |
| void | get_swapped_endian (T &x) |
| Conversion between little and big endian. Goes both ways. | |
| void | reversed_read (void *dest, size_t size, size_t nitems, std::ifstream &f, bool reverse) |
| Reads from file in normal or reverse order. | |
| void | reversed_write (const void *src, size_t size, size_t nitems, std::ofstream &f, bool reverse=false) |
| Writes to a file in normal or reversed order. | |
Norms | |
We define a number of standard, 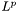 , norms on VectorD. , norms on VectorD.
| |
| template<unsigned int D> | |
| double | get_l1_norm (const VectorD< D > &v) |
| template<unsigned int D> | |
| double | get_l2_norm (const VectorD< D > &v) |
| template<unsigned int D> | |
| double | get_linf_norm (const VectorD< D > &v) |
Shortest segments | |
These methods return the shortest segment connecting two geometric objects. Such segments can be used to give the direction of the derivative of the distance between the two objects. The 0 point on the segment is in the first passed object and the 1 point is in the second. | |
| Segment3D | get_shortest_segment (const Segment3D &sa, const Segment3D &sb) |
| Segment3D | get_shortest_segment (const Segment3D &s, const VectorD< 3 > &p) |
Simple geometric IO | |
These functions write geometry to text files, one line per geometric primitive. Each line has the form “x y z” for points or “x y z r” for spheres. We can easily add general dimension support if requested.. Lines beginning with "#" are treated as comments. | |
| std::vector< VectorD< 3 > > | read_pts (TextInput in) |
| Read a set of 3D vectors from a file. | |
| std::vector< SphereD< 3 > > | read_spheres (TextInput in) |
| Read a set of 3d spheres from a file. | |
| void | write_pts (const std::vector< VectorD< 3 > > &vs, TextOutput out) |
| Write a set of 3D vectors to a file. | |
| void | write_spheres (const std::vector< VectorD< 3 > > &vs, TextOutput out) |
| Write a set of 3d spheres to a file. | |
Variables | |
| Matrix2D = _Matrix2D | |
| Matrix2D_f = _Matrix2D_f | |
| Matrix3D = _Matrix3D | |
| Matrix3D_f = _Matrix3D_f | |
| MultiArray2D_f = _MultiArray2D_f | |
| MultiArray3D = _MultiArray3D | |
| MultiArray3D_f = _MultiArray3D_f | |
| typedef BoundingBoxD<3> IMP::algebra::BoundingBoxD< 3 > |
See BoundingBoxD.
| Transformation3D compose | ( | const Transformation3D & | a, | |
| const Transformation3D & | b | |||
| ) |
compose two transformations
For any vector v (a*b)*v = a*(b*v).
| Transformation2D compose | ( | const Transformation2D & | a, | |
| const Transformation2D & | b | |||
| ) |
compose two transformations
For any vector v (a*b)*v = a*(b*v).
| Rotation2D IMP::algebra::compose | ( | const Rotation2D & | a, | |
| const Rotation2D & | b | |||
| ) |
compose two rotations a and b
For any vector v (a*b)*v = a*(b*v).
| bool IMP::algebra::get_are_almost_equal | ( | const double | a, | |
| const double | b, | |||
| const double | epsilon | |||
| ) |
Compares two values (intended for doubles).
epsilon is the tolerance allowed to consider the values as equal
| std::pair< VectorD< 3 >, double > get_axis_and_angle | ( | const Rotation3D & | rot | ) |
Decompose a Rotation3D object into a rotation around an axis.
www.euclideanspace.com/maths/geometry/rotations/conversions/ angleToQuaternion/index.htm
| double get_ball_radius_from_volume_3d | ( | double | volume | ) |
Return the radius of a sphere with a given volume.
<3>
| VectorD< D > get_basis_vector_d | ( | unsigned int | coordinate | ) |
Return the basis vector for the given coordinate.
Return the unit vector pointing in the direction of the requested coordinate. That is
get_basis_vector_d<3>(2)== VectorD<3>(0,0,1);
| VectorD< 3 > get_centroid | ( | const std::vector< VectorD< 3 > > & | ps | ) |
Returns the centroid of a set of vectors.
<3>
| std::string IMP::algebra::get_data_path | ( | std::string | file_name | ) |
Return the path to installed data for this module.
Each module has its own data directory, so be sure to use the version of this function in the correct module. To read the data file "data_library" that was placed in the data directory of module "mymodule", do something like
std::ifstream in(IMP::mymodule::get_data_path("data_library"));
IMP is installed or used via the tools/imppy.sh script.
| double get_distance | ( | const SphereD< D > & | a, | |
| const SphereD< D > & | b | |||
| ) |
Return the distance between the two spheres if they are disjoint.
If they intersect, the distances are not meaningful.
| double get_distance | ( | const Segment3D & | a, | |
| const Segment3D & | b | |||
| ) |
Get the distance between two segments.
| double get_distance | ( | const Segment3D & | s, | |
| const VectorD< 3 > & | p | |||
| ) |
Get the distance between a segment and a point.
| double get_distance | ( | const Rotation3D & | r0, | |
| const Rotation3D & | r1 | |||
| ) |
Return a distance between the two rotations.
The distance runs between 0 and 1. More precisely, the distance returned is the angle from the origin of the two quaternion vectors (with signs chosen appropriately), divided by pi/2.
| double get_distance | ( | const Plane3D & | pln, | |
| const VectorD< 3 > & | p | |||
| ) |
Return the distance between a plane and a point in 3D.
| SphereD< 3 > get_enclosing_sphere | ( | const std::vector< VectorD< 3 > > & | ss | ) |
Return a sphere containing the listed spheres.
<3> <3>
| SphereD< 3 > get_enclosing_sphere | ( | const std::vector< SphereD< 3 > > & | ss | ) |
Return a sphere containing the listed spheres.
<3>
| std::string IMP::algebra::get_example_path | ( | std::string | file_name | ) |
Return the path to installed example data for this module.
Each module has its own example directory, so be sure to use the version of this function in the correct module. For example to read the file example_protein.pdb located in the examples directory of the IMP::atom module, do
IMP::atom::read_pdb(IMP::atom::get_example_path("example_protein.pdb", model));
IMP is installed or used via the tools/imppy.sh script.
| FixedXYZ IMP::algebra::get_fixed_xyz_from_rotation | ( | const Rotation3D & | r | ) |
The inverse of rotation_from_fixed_xyz().
| FixedZYZ get_fixed_zyz_from_rotation | ( | const Rotation3D & | r | ) |
The inverse of rotation_from_fixed_zyz().
| const VectorD<3>& IMP::algebra::get_geometry | ( | const VectorD< 3 > & | v | ) |
| Rotation3D get_identity_rotation_3d | ( | ) |
Return a rotation that does not do anything.
| Transformation3D get_identity_transformation_3d | ( | ) |
Return a transformation that does not do anything.
| T IMP::algebra::get_linearly_interpolated | ( | double | diff, | |
| T | lower, | |||
| T | upper | |||
| ) |
Simple interpolation that is only valid for values of a ranging from 0 to 1.
| VectorD< 3 > get_orthogonal_vector | ( | const VectorD< 3 > & | v | ) |
Return a vector that is perpendicular to the given vector.
Or, if you are Israeli, it is a vertical vector. <3>
| double get_power_distance | ( | const SphereD< D > & | a, | |
| const SphereD< D > & | b | |||
| ) |
Return the power distance between the two spheres.
The power distance is the square of the distance between the centers minus the sum of the square of the radii.
| std::vector<VectorD<3> > IMP::algebra::get_random_chain | ( | unsigned int | n, | |
| double | r, | |||
| const VectorD< 3 > & | start = Vector3D(0, 0, 0), |
|||
| const std::vector< SphereD< 3 > > & | obstacles = Sphere3Ds() | |||
| ) |
Generate a random chain with no collisions.
This function generates a random chain, starting at (0,0,0) with n particles each with radius r. Consecutive particles are approximately distance 2r apart and no pair of particles is closer than 2r.
If an obstacles parameter is provided then chain spheres also don't intersect the obstacle spheres.
| Rotation3D get_random_rotation_3d | ( | const Rotation3D & | center, | |
| double | distance | |||
| ) |
Pick a rotation at random near the provided one.
This method generates a rotation that is within the provided distance of center.
| [in] | center | The center of the rotational volume |
| [in] | distance | See get_distance(const Rotation3D&,const Rotation3D&) for a full definition. |
| Rotation3D get_random_rotation_3d | ( | ) |
Pick a rotation at random from all possible rotations.
| Transformation3D get_rotation_about_point | ( | const VectorD< 3 > & | point, | |
| const Rotation3D & | rotation | |||
| ) |
Generate a Transformation3D object from a rotation around a point.
Rotate about a point rather than the origin.
| [in] | point | Center to rotate about |
| [in] | rotation | The rotation to perform |
| Transformation2D get_rotation_about_point | ( | const VectorD< 2 > & | point, | |
| const Rotation2D & | rotation | |||
| ) |
Generates a Transformation2D object from a rotation around a point.
Generates a Transformation2D to rotate about a point rather than the origin.
| [in] | point | Center to rotate about |
| [in] | rotation | The rotation to perform (defined taking the origin as reference, not the new point). |
| Rotation3D get_rotation_from_fixed_xyz | ( | double | xr, | |
| double | yr, | |||
| double | zr | |||
| ) |
Initialize a rotation in x-y-z order from three angles.
| [in] | xr | Rotation around the X axis in radians |
| [in] | yr | Rotation around the Y axis in radians |
| [in] | zr | Rotation around the Z axis in radians |
| Rotation3D get_rotation_from_fixed_zxz | ( | double | phi, | |
| double | theta, | |||
| double | psi | |||
| ) |
Initialize a rotation from euler angles.
| [in] | phi | Rotation around the Z axis in radians |
| [in] | theta | Rotation around the X axis in radians |
| [in] | psi | Rotation around the Z axis in radians |
| Rotation3D get_rotation_from_fixed_zyz | ( | double | Rot, | |
| double | Tilt, | |||
| double | Psi | |||
| ) |
Generate a rotation object from Euler Angles.
| [in] | Rot | First Euler angle (radians) defining the rotation (Z axis) |
| [in] | Tilt | Second Euler angle (radians) defining the rotation (Y axis) |
| [in] | Psi | Third Euler angle (radians) defining the rotation (Z axis) |
| Rotation3D get_rotation_from_vector4d | ( | const VectorD< 4 > & | v | ) |
Compute a rotatation from an unnormalized quaternion.
| Rotation3D get_rotation_in_radians_about_axis | ( | const VectorD< 3 > & | axis, | |
| double | angle | |||
| ) |
Generate a Rotation3D object from a rotation around an axis.
| [in] | axis | the rotation axis passes through (0,0,0) |
| [in] | angle | the rotation angle in radians |
www.euclideanspace.com/maths/geometry/rotations/conversions/ angleToQuaternion/index.htm
| Rotation2D IMP::algebra::get_rotation_to_x_axis | ( | const VectorD< 2 > & | v | ) |
Builds the rotation that transforms the vector X of the origin of coordinates into the given vector
| int IMP::algebra::get_rounded | ( | const T & | x | ) |
Rounds a number to next integer.
The result is of type integer but the argument can be of any type. Some examples:
a = round(-0.7); // a = -1 a = round(-0.2); // a = 0 a = round(0.2); // a = 0 a = round(0.7); // a = 1
| Segment3D get_shortest_segment | ( | const Segment3D & | s, | |
| const VectorD< 3 > & | p | |||
| ) |
<3>
| Transformation3D IMP::algebra::get_transformation_3d | ( | const Transformation2D & | t2d | ) |
Builds a 3D transformation from a 2D one.
| IMP::algebra::Transformation3D get_transformation_aligning_first_to_second | ( | const Vector3DsOrXYZs0 & | from, | |
| const Vector3DsOrXYZs1 & | to | |||
| ) |
Compute the rigid transform bringing the first point set to the second.
The points are assumed to be corresponding (that is, from[0] is aligned to to[0] etc.). The alignment computed is that which minimized the sum of squared distances between corresponding points. Return the
![\[ \operatornamewithlimits{argmin}_T \sum \left|T\left(f\left[i\right]\right)-t[i]\right|^2 \]](form_4.png)
If the point sets lie in a 1 or 2 dimensional subspace, the alignment algorithm is unstable and not guaranteed to work. A warning is printed in this case.
| Transformation2D IMP::algebra::get_transformation_aligning_pair | ( | const std::vector< VectorD< 2 > > & | set_from, | |
| const std::vector< VectorD< 2 > > & | set_to | |||
| ) |
Builds the transformation required to obtain a set of points from the first one
| Transformation3D get_transformation_from_reference_frame | ( | const VectorD< 3 > & | u, | |
| const VectorD< 3 > & | w, | |||
| const VectorD< 3 > & | base | |||
| ) |
A rotation from the natural reference frame to one defined by u,w and base. The x-axis lies on u-base. The y-axis is perpendicular to both x and z. The z-axis is perpendicular to the u-base , w-base plane.
Generate a transformation from the natural reference-frame to a different one
| [in] | u | vector used to define the new reference frame |
| [in] | w | vector used to define the new reference frame |
| [in] | base | the center of the new reference frame |
| Rotation3Ds IMP::algebra::get_uniform_cover_rotations_3d | ( | unsigned int | num_points | ) |
Cover the space of rotations evenly.
If you care about the distance between samples instead of the number of samples, the "surface area" of the set of rotations is pi^2. If you allocate each sample a volume of 4/3 pi d^3 (to space them d apart), Then you want 3/4 pi/d^3 points.
Creates at least num_points rotations.
| std::vector< VectorD< 3 > > get_uniform_surface_cover | ( | const SpherePatch3D & | sph, | |
| unsigned int | number_of_points | |||
| ) |
Generate a set of 3d points that uniformly cover a patch of a sphere.
| std::vector< VectorD< D > > get_uniform_surface_cover | ( | const SphereD< D > & | s, | |
| unsigned int | n | |||
| ) |
Generate a set of vectors which covers a sphere uniformly.
The function is currently pretty slow, especially in non-optimized builds. Complain if this bugs you. We might be able to do better, at least in 3D.
Creates at least the requested number of points.
| std::vector<VectorD<D> > IMP::algebra::get_uniform_upper_hemisphere_cover | ( | const SphereD< D > & | s, | |
| unsigned int | n | |||
| ) |
Generate a set of 3D points that uniformly cover a hemisphere.
The points all lie on the upper hemisphere, eg, all their z coordinates are greater than those of the center of the sphere.
| VectorD< 3 > get_vector_product | ( | const VectorD< 3 > & | p1, | |
| const VectorD< 3 > & | p2 | |||
| ) |
Returns the vector product (cross product) of two vectors.
<3>
| Rotation3D interpolate | ( | const Rotation3D & | a, | |
| const Rotation3D & | b, | |||
| double | f | |||
| ) |
Interpolate between two rotations.
It f ==0, return b, if f==1 return a.
| T IMP::algebra::linear_interpolation | ( | H & | v, | |
| int | size, | |||
| double | idx | |||
| ) |
Linear interpolation for a point in a vector.
| [in] | v | any class similar to a vector accessed by [] |
| [in] | size | number of elements in v |
| [in] | idx | index which value to interpolate |
| VectorD< D > operator* | ( | double | s, | |
| const VectorD< D > & | o | |||
| ) |
| std::vector< VectorD< 3 > > read_pts | ( | TextInput | in | ) |
| std::vector< SphereD< 3 > > read_spheres | ( | TextInput | in | ) |
| void IMP::algebra::reversed_read | ( | void * | dest, | |
| size_t | size, | |||
| size_t | nitems, | |||
| std::ifstream & | f, | |||
| bool | reverse | |||
| ) |
Reads from file in normal or reverse order.
If the reverse parameter is true, the data will be read in reverse order.
| void IMP::algebra::reversed_write | ( | const void * | src, | |
| size_t | size, | |||
| size_t | nitems, | |||
| std::ofstream & | f, | |||
| bool | reverse = false | |||
| ) |
Writes to a file in normal or reversed order.
This function is the same as fread from C, but at the end there is a flag saying if data should be read in reverse order or not.
If the reverse parameter is true, the data will be written in reverse order.
| void write_pts | ( | const std::vector< VectorD< 3 > > & | vs, | |
| TextOutput | out | |||
| ) |
| void write_spheres | ( | const std::vector< VectorD< 3 > > & | vs, | |
| TextOutput | out | |||
| ) |